Overview
Approximating bezier curves by circular arcs, in spite of how useless it sounds regarding modern drawing APIs, has (at least) one raison d’etre. The G-Code language used by most CNC machines, and also adopted by most 3D printers, can deal with linear interpolation (lines) and circular interpolation (circular arcs) only.
I have been working recently on a simple Haskell SVG to G-Code converter, and I realized, that in spite of the simplicity of the algorithm at the end, how confusing the subject is (partly because of some not very well written research paper(s) delivered by google search on the subject).
The algorithm explained in this post is implemented in C# and can be found at my GitHub repository. The C# code is only for illustrating the algorithm, later on it will be integrated with my Haskell SVG to G-Code project.
The article assumes that you understand basic algebra and geometry, complex numbers, etc…
Bezier curves
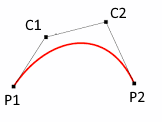
I assume that you already familiar with bezier curves, here I want to introduce only the notations used in this post. We restrict ourselves to cubic bezier curves (it is not a real limitation, any quadratic bezier curve can be straightforwardly converted to a cubic bezier curve). P1 denotes the start point, P2 the end point, and C1, C2 the control points of the start and end points, respectively. Because it is important for the algorithm, please remember that the line denoted by P1 and C1 is the tangent at P1, and, similarly, the line denoted by P2 and C2 is the tangent at P2.
Biarcs

A biarc is a pair of circular arcs (= two arcs) which have the same tangent at the connection point they meet. We will use one biarc to approximate a bezier segment which has no inflection point. A traditional biarc approximation task has four parameters: a start point, an end point, and the tangents at these points. Using these four parameters, however, is not enough to uniquely identify a biarc, we need one more parameter: this can be e.g. the connection point of the arcs or the tangent at the connection point.
Before we start
This algorithm works on bezier curves without any inflection points. Thus, as a preliminary step, the inflection points must be found and the curve must be split (the parts will be approximated one by one). It is a simple task though. We just have to find the points where the second derivative of the parametric equation of the bezier curve becomes zero. It is a quadratic equation, so that can happen at no more than two points. Obviously, we will be interested in the real (not complex) solutions only and only which are in the [0,1] interval. For the details please contact with the implementation.
The biarc fitting
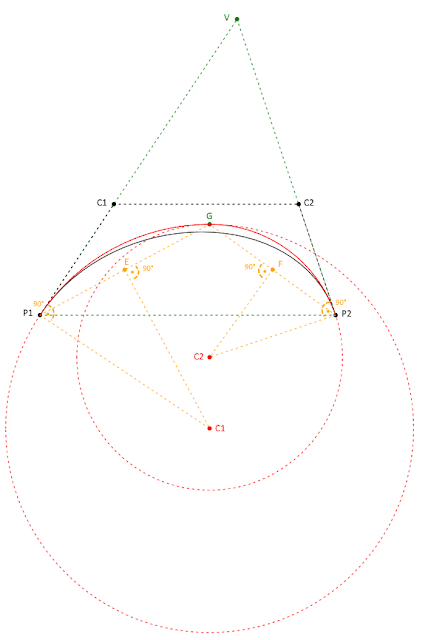
We have a simple cubic bezier curve at this point, and we want to approximate it with a biarc. For that we need one more parameter. Some research suggests [1] that in the case of bezier curves, the connection point of the arcs of the biarc should be the incenter point of the triangle denoted by the points P1, P2, and V, where V is the intersection point of the tangents at P1 and P2. Let’s call this incenter point G.
For illustration, see the image at the bottom of the article. Black color is related to the original bezier curve, green color is related to the incenter point, red color is related to the approximation biarc, and yellow color is related to the arc computations as it is explained in the following paragraph.
The next step is to find the two circles on which the arcs lie. We have three clues per circle. Circle 1: its two points P1 and G, and the tangent at P1. Circle 2: its two points G and P2, and the tangent at P2.
To be done, we need to find C1 and C2, the center points of these circles.
It is simple. We know the tangent at P1. C1 lies on the line which is perpendicular to this tangent and goes through P1, let’s denote it by P1C. If we take the section between P1 and G, its perpendicular bisector (EC1) intersects with P1C at C1. The same method can be used to find C2.
Estimate the error and go recursive
Obviously, as you can also see on the illustration, most of the time the approximation is not close enough. Thus, after approximation, the error must be estimated, and if it is out of the tolerance range the bezier curve must be split, then the two new bezier curves must be approximated recursively until you reach an acceptable deviation. In my implementation I just simply check the distance at a certain number of points along the curve and split if the maximum deviation is not acceptable (the bezier curve is split where the deviation is the maximum as suggested by [2]). This is certainly not fast, but acceptable for my purposes.
For what project do you want to use bezier approximation?